Gini coefficient algorithm
10 Aug 2024In economics, the Gini coefficient (or Gini index) is a measure of inequality of a dataset. It usually represents income inequality or wealth inequality. I stumbled upon this concept while reading this Go code which I was confused at the first look. This posting is my attempt to understand the code.
// calculate gini coefficient
sumOfAbsoluteDifferences := float64(0)
subSum := float64(0)
for i, x := range stakingAmount {
temp := x*float64(i) - subSum
sumOfAbsoluteDifferences = sumOfAbsoluteDifferences + temp
subSum = subSum + x
}
result := sumOfAbsoluteDifferences / subSum / float64(len(stakingAmount))
Geometric definition
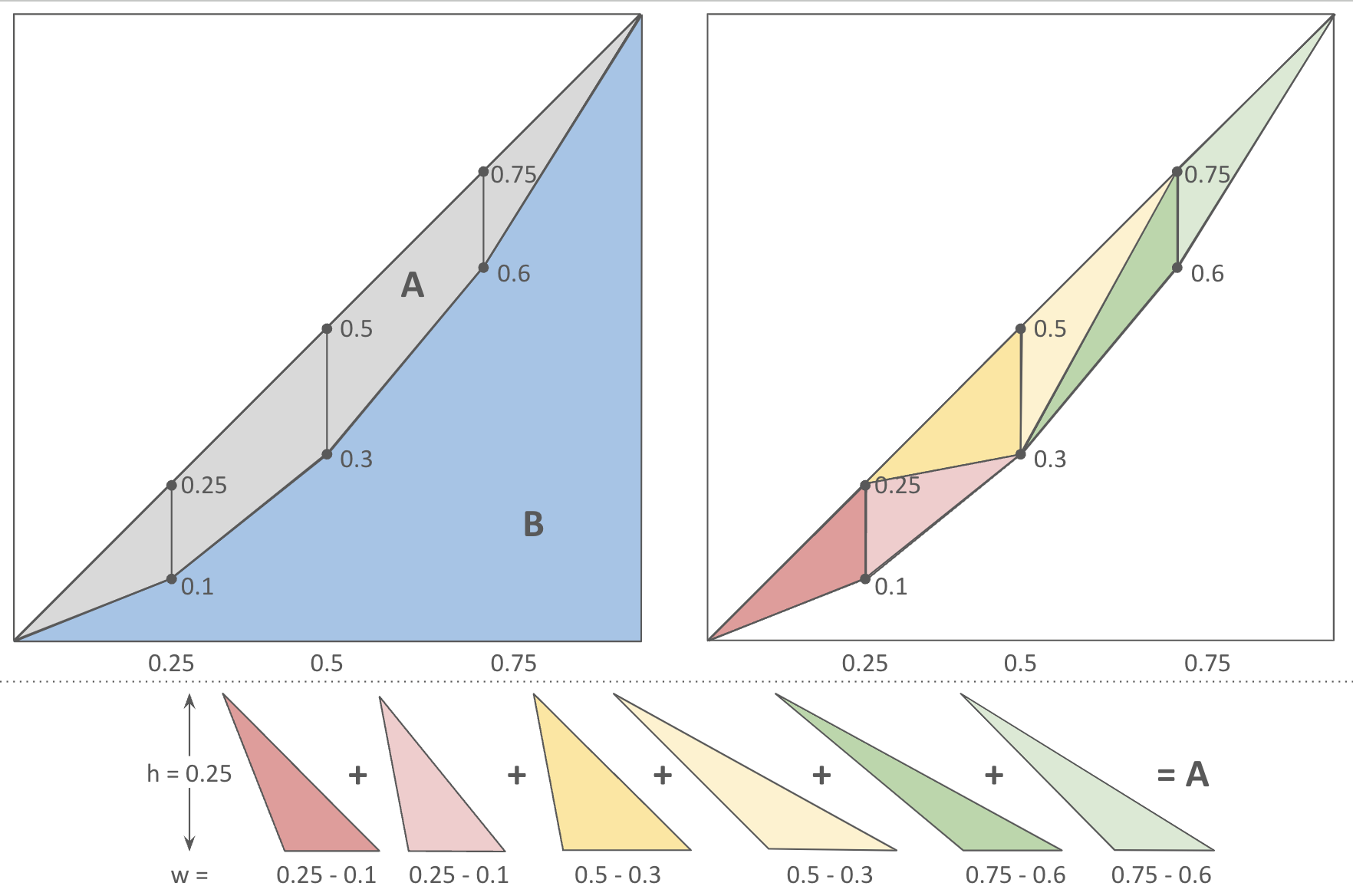
The Gini is a number between 0 to 1, that is defined using the Lorenz curve. Lorenz curve plots the cumulative share of data points sorted in ascending order. In the diagram below, the Gini is defined using the two areas A and B (since $A+B = 1/2$),
\[G = A / (A+B) = 2A\]Consider a dataset with four data points, 1, 2, 3, 4. Then,
- the sequence of cumulative sum is
1, 3, 6, 10. - the sequence of cumulative share is
0.1, 0.3, 0.6, 1.0, the cumulative sums divided by the total sum, 10.
The area between the curve and line, A, can be calculated by calculating the areas of below 6 triangles. Each triangle has the same height 0.25.