Regex Crossword Solver with Z3

1. Problem Statement

Regex Crossword (https://regexcrossword.com/) is a crossword puzzle where you fill in a rectangular board, so that regular expressions on every row and column are satisfied. It looks like this.

During fun geeky solving time, I thought it could be solved with computer. And actually there are great works with Regex Crossword solvers.

Herman Schaaf has solved it in Go-lang (http://herman.asia/solving-regex-crosswords-using-go). His solution analyzes the DFA generated by Go-lang’s regular expression compiler. His solution solves it really fast, that it only takes few miliseconds to solve one, but it cannot deal with backreferences.

Thomas Parslow has solved hexagonal version in Haskell (http://almostobsolete.net/regex-crossword/part1.html). His approach is basically same as solving by hand. He wrote a custom regular expression engine to do that. His solution can solve ones with backreferences, very quickly.

I’ve decided to take another approach, using SMT solver.

2. Z3 SMT Solver

SMT problem is a extended version of SAT problem. Given a formula, checking if there is a set of values for variables that satisfies the formula. The difference is, that SAT only deals with boolean expressions, whereas SMT can handle various types such as integer, bit vector and real number.

Depending on which theory to use, you can express constraints in different formats. This time, we will use linear integer arithmetic, where equations in the SMT problems are linear equations over integer variables.

There are many SMT Solvers, but I chose Z3 because it is well documented and is ported to Python language. It’s really easy to use. Take a look at an example:

>>> import z3
>>> x = z3.Int('x')
>>> y = z3.Int('y')
>>> solver = z3.Solver()
>>> solver.add(x + y == 10)
>>> solver.add(x - y == 4)
>>> solver.check()
sat
>>> solver.model()
[x = 7, y = 3]

Download Z3 here: https://github.com/Z3Prover/z3
And Z3Py documentation is here: http://www.cs.tau.ac.il/~msagiv/courses/asv/z3py/guide-examples.htm

3. Solution overview

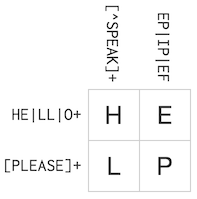
A Regex Crossword puzzle consists of multiple blanks and multiple regular expressions. Above example consists of four unknowns and four regular expressions. We could write like this.

Unknowns: x00, x01, x10, x11.
Constraints:
  [x00, x01] is accepted by HE|LL|O+
  [x10, x11] is accepted by [PLEASE]+
  [x00, x10] is accepted by [^SPEAK]+
  [x10, x11] is accepted by EP|IP|EF

Then the first constraint can be written like

(x00==H && x01==E) || (x00==L && x01==L) || (x00=O && x01=O)

I wanted to automate this translation process. If I do that, then I can generate SMT problem that are equivalent to the Regex Crossword puzzle. The solution for the SMT problem (solved by Z3) is the solution to the puzzle.

4. Translating regex constraints into SMT problem

Given string length N and regular expression r, what we want to find is, in short,

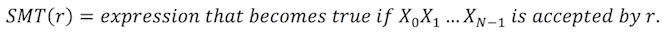
Before calculating this directly, I’ve defined two functions. First one is LEN(regex).

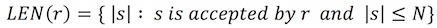
It is set of lengths of the strings, that are matched by r. For example, LEN("ab(c|de).") = {4,5}. Some regular expressions like ABC* has infinite number of possibilities in its length. But since we are dealing with fixed length string, we ignore the lengths exceeding N. Then LEN can be calculated recursively like this.

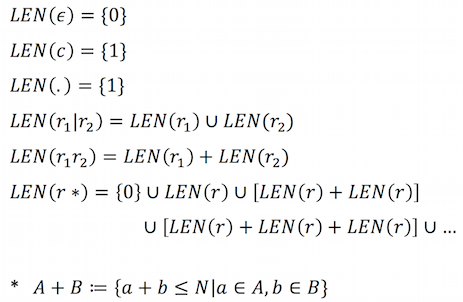
After we have LEN, we define generalized version of SMT.

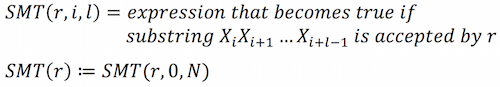
SMT is calculated recursively like this.

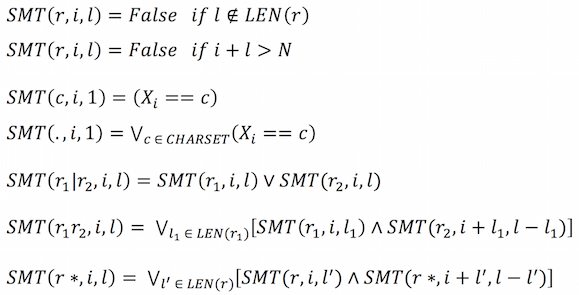
For example, finding a length-3 string accepted by A(B|C)*D* can be written as:

Or(And(x0 == 65, x1 == 68, x2 == 68),
   And(x0 == 65, Or(x1 == 66, x1 == 67), x2 == 68),
   And(x0 == 65,
       Or(x1 == 66, x1 == 67),
       Or(x2 == 66, x2 == 67)))

5. Handling Backreferences

Backreferences made it difficult. Backreference allows us to match a previously matched group. For example, (a.)zzz\1 matches abzzzab.

Previous divide and conquer strategy was not enough for backrefs. I solved it by adding position variables p_m. They are hidden integer variables in the SMT problem that represent the positions of previously matched groups. With these, our calculations of LEN and SMT are updated as follows.

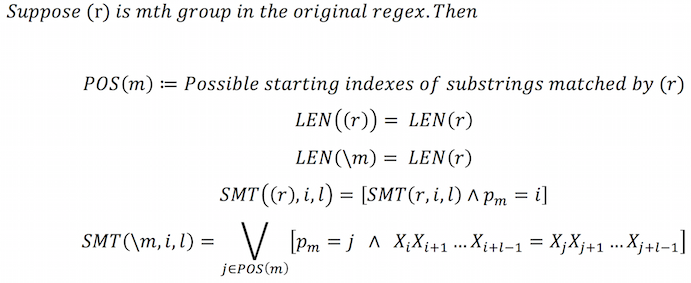
For example, finding a length-3 string accepted by X*(A|B)\1Y* can be written as following SMT problem.

Or(And(p_0 == 0, Or(x0 == 65, x0 == 66), x1 == x0, x2 == 89),
   And(x0 == 88,
       p_0 == 1,
       Or(x1 == 65, x1 == 66),
       Or(And(p_0 == 0, x2 == x0), And(p_0 == 1, x2 == x1))))

You can see that the expression consists of two cases, which are p_0 being 0 and 1. p_0 is position variable for first group (A|B).

6. Handling extended syntaxes

Regex has rich syntaxes. I simply replaced them into equivalent basic syntaxes. Namely,

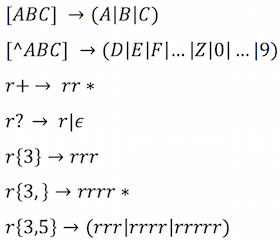
7. Conclusion

I’ve coded this method in Python using Python Lex-Yacc and Z3Py.

>>> import crossword
>>> crossword.solve_crossword(["HE|LL|O+","[PLEASE]+"], ["[^SPEAK]+","EP|IP|EF"])
[['H', 'E'], ['L', 'P']]

My code is available here.