Gini coefficient algorithm
10 Aug 2024In economics, the Gini coefficient (or Gini index) is a measure of inequality of a dataset. It usually represents income inequality or wealth inequality. I stumbled upon this concept while reading this Go code which I was confused at the first look. This posting is my attempt to understand the code.
// calculate gini coefficient
sumOfAbsoluteDifferences := float64(0)
subSum := float64(0)
for i, x := range stakingAmount {
temp := x*float64(i) - subSum
sumOfAbsoluteDifferences = sumOfAbsoluteDifferences + temp
subSum = subSum + x
}
result := sumOfAbsoluteDifferences / subSum / float64(len(stakingAmount))
Geometric definition
The Gini is a number between 0 to 1, that is defined using the Lorenz curve. Lorenz curve plots the cumulative share of data points sorted in ascending order. In the diagram below, the Gini is defined using the two areas A and B (since $A+B = 1/2$),
\[G = A / (A+B) = 2A\]Consider a dataset with four data points, 1, 2, 3, 4. Then,
- the sequence of cumulative sum is
1, 3, 6, 10. - the sequence of cumulative share is
0.1, 0.3, 0.6, 1.0, the cumulative sums divided by the total sum, 10.
The area between the curve and line, A, can be calculated by calculating the areas of below 6 triangles. Each triangle has the same height 0.25.
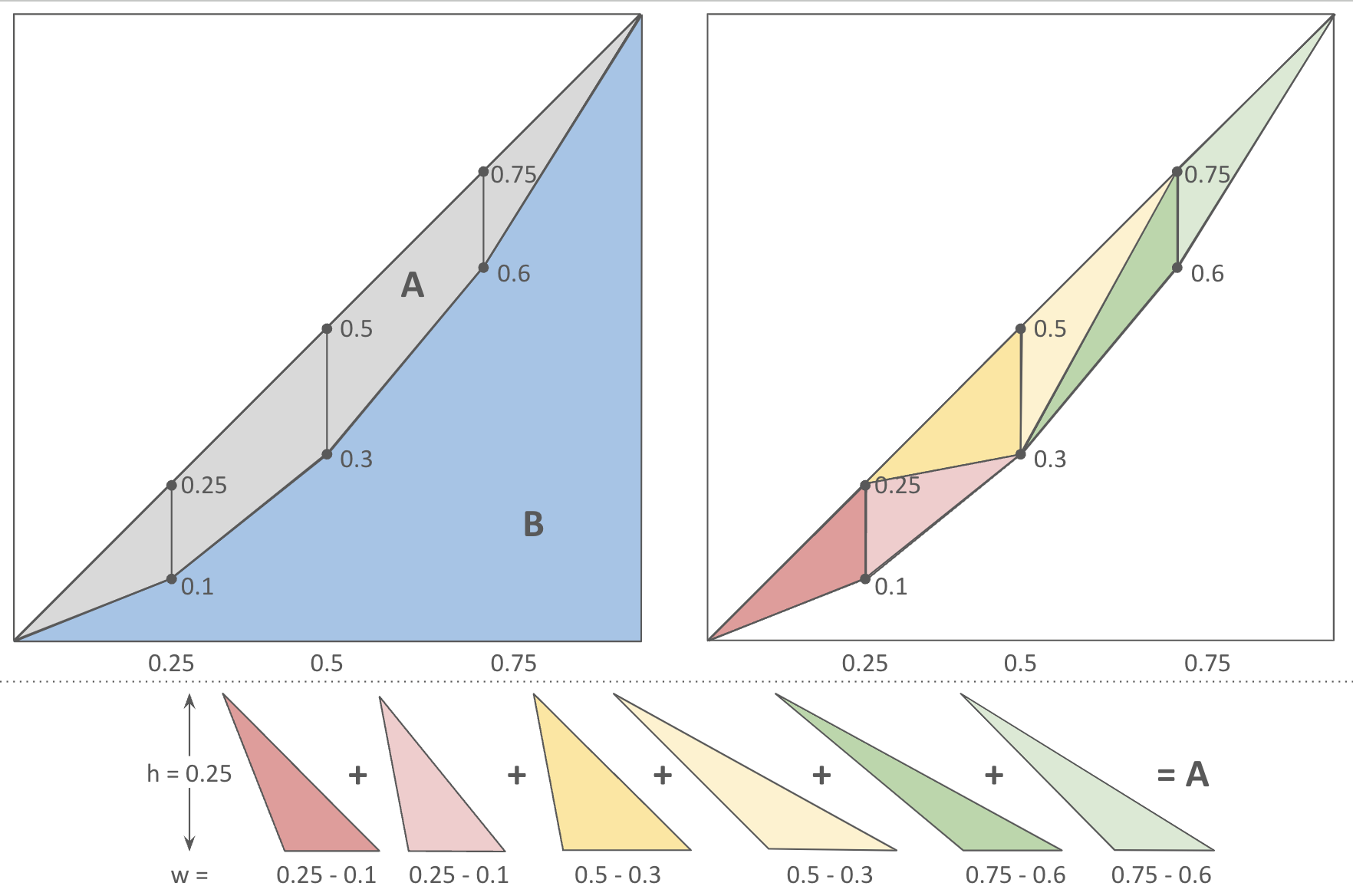
Because area of a triangle is $\frac{1}{2}wh$ and every couple of triangles have the same width,
\[A = 0.25\times\left[(0.25-0.1) + (0.5-0.3) + (0.75-0.6)\right] = 0.125\]Therefore the Gini coefficient
\[G = 2A = 0.25\]Reshaping the formula
Let us replace the numbers with symbols.
- Number of elements $n = 4$
- Each element $a,b,c,d = y_0,y_1,y_2,y_3 = 1,2,3,4$ (index starts from 0)
- Cumulative sums $s_1,s_2,s_3,s_4 = 1,3,6,10$ ($s_k$ is sum of $k$ elements)
- Total sum $S=10$ ($S = \sum y_i$)
Then we can rewrite the areas of triangles:
\[A = \frac{1}{n}\left[ \left(\frac{1}{n}-\frac{s_1}{S}\right) + \left(\frac{2}{n}-\frac{s_2}{S}\right) + \left(\frac{3}{n}-\frac{s_3}{S}\right) \right]\]Add one last term which computes to 0 because $(4/n - s_4/S) = (1 - 1) = 0$.
\[A = \frac{1}{n}\left[ \left(\frac{1}{n}-\frac{s_1}{S}\right) + \left(\frac{2}{n}-\frac{s_2}{S}\right) + \left(\frac{3}{n}-\frac{s_3}{S}\right) + \left(\frac{4}{n}-\frac{s_4}{S}\right) \right]\]Simplify using the formula $1+2+..+n = n(n+1)/2$,
\[\begin{aligned} nA &= \frac{1+2+3+4}{n} - \frac{1}{S}(s_1 + s_2 + s_3 + s_4) \\ nA &= \frac{n+1}{2} - \frac{1}{S}(s_1 + s_2 + s_3 + s_4) \\\\ 2nSA &= S(n+1) - 2(s_1 + s_2 + s_3 + s_4) \end{aligned}\]Rearrange the terms,
\[2nSA = \text{sum}\begin{pmatrix} S-2S_1 \\ S-2S_2 \\ S-2S_3 \\ S-2S_4 \\ S \end{pmatrix} = \text{sum}\begin{pmatrix} a+b+c+d - 2(a)\qquad\qquad\qquad \\ a+b+c+d - 2(a+b)\qquad\qquad \\ a+b+c+d-2(a+b+c)\qquad \\ a+b+c+d-2(a+b+c+d) \\ a+b+c+d\qquad\qquad\qquad\qquad \end{pmatrix} = \text{sum}\begin{pmatrix} -a+b+c+d \\ -a-b+c+d \\ -a-b-c+d \\ -a-b-c-d \\ +a+b+c+d \end{pmatrix}\]Cancel out the diagonal $(-a -b -c -d)$ against the bottom row $(+a +b +c +d)$,
\[2nSA = \text{sum}\begin{pmatrix} \qquad +b+c+d \\ -a\qquad+c+d \\ -a-b\qquad+d \\ -a-b-c\qquad \end{pmatrix}\]Group by the positive term,
\[\begin{aligned} 2nSA &= \left[(b-a)\right] + \left[(c-a) + (c-b)\right] + \left[(d-a) + (d-b) + (d-c)\right] \\ &= [1b - s_1] + [2c - s_2] + [3d - s_3] \\ &= [1y_1 - s_1] + [2y_2 - s_2] + [3y_3 - s_3] \end{aligned}\]To generalize,
\[2nSA = \sum_{i=0}^{n-1}{i \cdot y_i - s_i}\]The Gini coefficient
\[G = 2A = \frac{1}{nS}\sum_{i=0}^{n-1}{i \cdot y_i - s_i}\]Statistical definition
An alternative definition of the Gini coefficient is half of relative mean absolute difference.
\[G = \frac{ \sum_{i=0}^{n-1}\sum_{j=0}^{n-1}|y_i - y_j| }{ 2n\sum_{i=0}^{n-1}y_i }\] \[2nSG = \sum_{i=0}^{n-1}\sum_{j=0}^{n-1}|y_i - y_j|\]The sum of $n \times n$ terms can be separated into three groups. Below is an example when $n=3$.
\[\begin{aligned} 2nSG &= \text{sum}\begin{pmatrix} |a-a|\ |a-b|\ |a-c| \\ |b-a|\ |b-b|\ |b-c| \\ |c-a|\ |c-b|\ |c-c| \end{pmatrix} \\ &= \text{sum}\begin{pmatrix} \\ |b-a|\qquad\quad \\ |c-a|\ |c-b| \end{pmatrix} + \text{sum}\begin{pmatrix} |a-a|\qquad\qquad \\ \qquad|b-b|\qquad \\ \qquad\qquad|c-c| \end{pmatrix} + \text{sum}\begin{pmatrix} |a-b|\ |a-c| \\ \qquad\quad|b-c| \\ \quad \end{pmatrix} \\ &= 2\times\text{sum}\begin{pmatrix} \\ |b-a|\qquad\quad \\ |c-a|\ |c-b| \end{pmatrix} \end{aligned}\]The diagonal is zero. The lower left and upper right are equal. So we only need to calculate the lower left and double it. Also note that the absolute sign is now unnecessary because elements are in ascending order.
\[nsG = \sum_{i=1}^{n-1}\sum_{j=0}^{i-1}|y_i - y_j| = \sum_{i=1}^{n-1} \left[ \sum_{j=0}^{i-1}(y_i - y_j) \right] = \sum_{i=1}^{n-1} \left[ i\cdot y_i - \sum_{j=0}^{i-1}y_j \right]\]Arriving at the same formula,
\[G = \frac{1}{nS}\sum_{i=0}^{n-1}{i \cdot y_i - s_i}\]Hence the original Go code, computing Gini in $O(n\,\text{log}\,n)$ time.
// calculate gini coefficient
sumOfAbsoluteDifferences := float64(0)
subSum := float64(0)
for i, x := range stakingAmount {
temp := x*float64(i) - subSum
sumOfAbsoluteDifferences = sumOfAbsoluteDifferences + temp
subSum = subSum + x
}
result := sumOfAbsoluteDifferences / subSum / float64(len(stakingAmount))